
Buffers
Acids and bases
A brief introduction
Buffers are a mixture og acids and their corresponding bases, e.g. acetic acid and acetate ions. Buffers have the ability to counteract changes in pH, e.g. for reactions producing acids or bases, thereby ensuring a more or less stable pH in the solution. The buffer effect is a property used e.g. in biological systems and industrial processes and advanced analysis.
On a titration curve, e.g. like this one for 5 ml acetic acid (1 M solution) with NaOH (1 M solution)
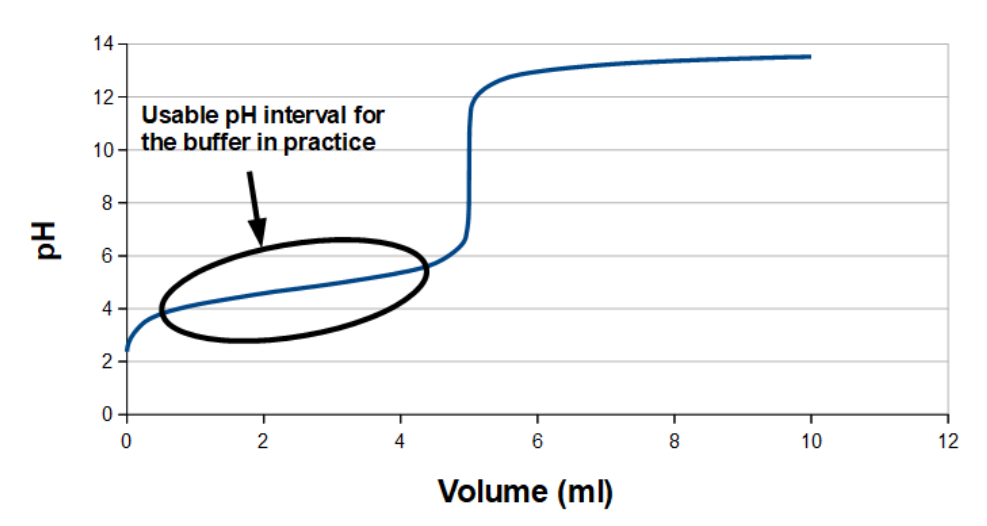
the solution is a buffer from when the titration is startet and up to right before equivalence point (at 5 ml NaOH solution).
In practice the usable interval for the buffer is a bit smaller, as marked on the titration curve. For buffers to work in practice, you have to operate in the concentration range where pH changes the least when adding acid or base, i.e. in the approximately linear area. To have a buffer effect which is as robust as possible, it is usually best if the limitations in you process window are not the same as the buffer's application range. It is safety measure in process technology, if an accident or something unpredicted happens while the chemical reaction in the buffer is taking place.
Obviously there is a limit to how much the buffer can counteract the amount of added acid or base. This is called the solution's buffer capacity and is dependent on the buffer's acid and base content. As there is usually not the same concentration of acid and base in the buffer, unless you are at the point where pH = pKa, you should be aware that the buffer's buffer capacity is not necessarily the same for acids and bases.
Because a buffer, e.g. like the acetate buffer, consisting of acetic acid and acetate, has a rather narrow pH interval where it works, you have a wide range of buffer systems, which is used, depending on the pH value you need to maintain for the reaction. You can find several buffer systems for a specific pH level, and you should beware of side reactions with the buffer, affecting the primary reaction. In applications like crystallization of macromolecules for x-ray crystallography, the difference in buffer type alone can be the difference between crystal formation or not.
Buffer types and their pH ranges is something you can look up, and you can buy kits, where you just pour the content of a bag into a specific amount of water, and the buffer is ready as soon as the content is dissolved.
On a titration curve, e.g. like this one for 5 ml acetic acid (1 M solution) with NaOH (1 M solution)

the solution is a buffer from when the titration is startet and up to right before equivalence point (at 5 ml NaOH solution).
In practice the usable interval for the buffer is a bit smaller, as marked on the titration curve. For buffers to work in practice, you have to operate in the concentration range where pH changes the least when adding acid or base, i.e. in the approximately linear area. To have a buffer effect which is as robust as possible, it is usually best if the limitations in you process window are not the same as the buffer's application range. It is safety measure in process technology, if an accident or something unpredicted happens while the chemical reaction in the buffer is taking place.
Obviously there is a limit to how much the buffer can counteract the amount of added acid or base. This is called the solution's buffer capacity and is dependent on the buffer's acid and base content. As there is usually not the same concentration of acid and base in the buffer, unless you are at the point where pH = pKa, you should be aware that the buffer's buffer capacity is not necessarily the same for acids and bases.
Because a buffer, e.g. like the acetate buffer, consisting of acetic acid and acetate, has a rather narrow pH interval where it works, you have a wide range of buffer systems, which is used, depending on the pH value you need to maintain for the reaction. You can find several buffer systems for a specific pH level, and you should beware of side reactions with the buffer, affecting the primary reaction. In applications like crystallization of macromolecules for x-ray crystallography, the difference in buffer type alone can be the difference between crystal formation or not.
Buffer types and their pH ranges is something you can look up, and you can buy kits, where you just pour the content of a bag into a specific amount of water, and the buffer is ready as soon as the content is dissolved.
pH calculations on buffers
pH calculations for buffers are done using the formula
or
as the total volume is the same for both acid and base, and thus removable by reduction.
How to approach the calculation, depends on the circumstances. If you are just mixing the acid with its corresponding base, in a specified ratio, you simply insert the amount of substance in moles or the concentrations, and do the calculation. Is it an acid or a base being titrated, you approach the problem as a stoichiometric calculation, before inserting the numbers in the formula. Let's take a look at a couple of examples:
If you take 0.50 l of a 1.00 M acetic acid (pKa=4,75), and add 20.50 g of anhydrous NaAc (0.25 mole), then n(HAc) = 0.50 mole, and we can calculate pH as
Instead it might be 0.50 l of a 0.50 M acetic acid solution, being titrated with 100 ml of a 1.00 M NaOH solution. In that case, you have to start with the reaction equation and the stoichiometric calculations. That part looks like this:
Now we can enter the values in the buffer formula:
It doesn't have to be pH you want to calculate. It could be an unknown pKa you want to determine, or the concentration of the acid and/or base in the solution, which is only a matter of inserting the known values in the equation and treat it like any other equation with one unknown.
| pH = pKa + log | [base] |
| [acid] |
or
| pH = pKa + log | n(base) |
| n(acid) |
as the total volume is the same for both acid and base, and thus removable by reduction.
How to approach the calculation, depends on the circumstances. If you are just mixing the acid with its corresponding base, in a specified ratio, you simply insert the amount of substance in moles or the concentrations, and do the calculation. Is it an acid or a base being titrated, you approach the problem as a stoichiometric calculation, before inserting the numbers in the formula. Let's take a look at a couple of examples:
If you take 0.50 l of a 1.00 M acetic acid (pKa=4,75), and add 20.50 g of anhydrous NaAc (0.25 mole), then n(HAc) = 0.50 mole, and we can calculate pH as
| pH = 4,75 + log | 0.25 mole | = 4.75 + log(0.50) = 4.5 |
| 0.50 mole |
Instead it might be 0.50 l of a 0.50 M acetic acid solution, being titrated with 100 ml of a 1.00 M NaOH solution. In that case, you have to start with the reaction equation and the stoichiometric calculations. That part looks like this:
| HAc(aq) | + | OH−(aq) |  | Ac−(aq) | + | H2O(l) | |
| Start | 0.25 mole | - | - | - | |||
| Added | - | 0.10 mole | - | - | |||
| End | 0.15 mole | 0.00 mole | 0.10 mole | 0.10 mole |
Now we can enter the values in the buffer formula:
| pH = 4.75 + log | 0.10 mole | = 4.75 + log(0.67) = 4.6 |
| 0.15 mole |
It doesn't have to be pH you want to calculate. It could be an unknown pKa you want to determine, or the concentration of the acid and/or base in the solution, which is only a matter of inserting the known values in the equation and treat it like any other equation with one unknown.