
Electrical resistivity and conductivity
Conductivity
Resistivity
For a metal conductor, the relationship between voltage V (occasionally written as E or U), resistance, R, and current, I, follows Ohm's law:
In some educational institutions, it is traditionally written like this U = R · I.
What is important to keep in mind here, is that Ohm's law is an idealized relationship, i.e. it describes the general relation quite well, in regards to metal conductors. However, as a general model for materials, it isn't correct.
Ohm's law can be extended to take the cross-section area, length and the material's conductivity into consideration. For a conductive material, having the cross-section area A, the length ℓ and resistivity ρ, the resistance R is:
Resistivity for a material is defined as the ratio between the electrical field, E, and current density, J:
The electric field and current density are proportionate at constant temperature, which is the original Ohm's Law, as discovered by G.S. Ohm. The SI unit for ρ is Ω ·m, and the practical aspect of resistivity is that a perfect conductor will have ρ = 0, i.e. no resistance (also called a superconductor), and a perfect insulator, on the other hand, will have ρ = ∞.
Materials following Ohm's Law are called ohmic conductors. Materials not following Ohm's Law are called non-Ohmic conductors.
If we look at resistivity from a practical point of view, these are actual values for some common and representative materials:
Note: Insulator does not mean that the material cannot conduct a current, it means that it is a very poor conductor! The difference becomes relevant when working e.g. with strong current. The line between what is considered a semiconductor and is considered an insulator is not clear, but in practice, line between conductor and semiconductor is around 10−5 Ω·cm, and the transition to insulator is around 107 Ω·cm
Resistivity is dependent on both temperature and material, and you see the following three dependencies:
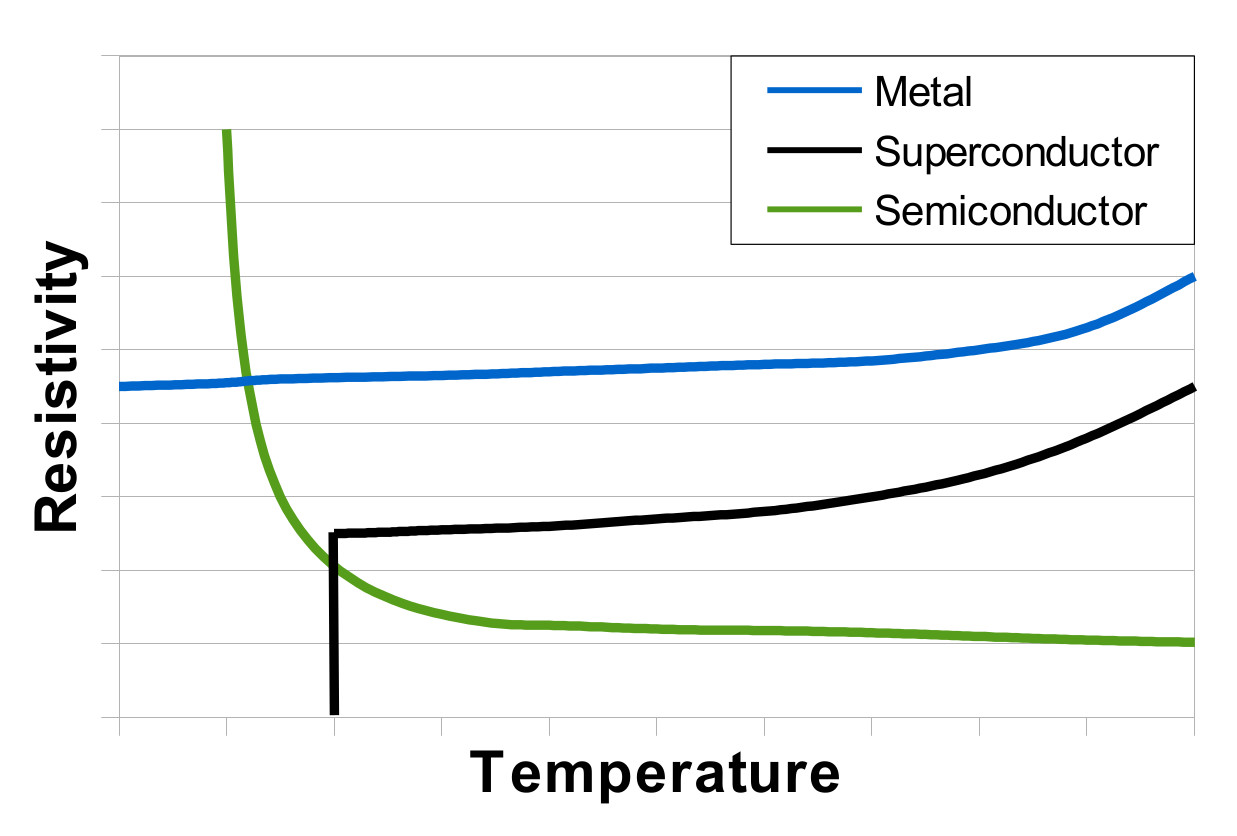
Metallic conductors
In general for metallic conductors, resistivity increases with temperature. For moderate temperature intervals, the change in resistivity can be calculated using the following approximation:
Superconductors
Resistivity decreases with decreasing temperature in the beginning, like for the metals, but at a specific transition temperatures for the material, usually around 0.1 to K, a phase transition occurs in the material and resistivity abruptly drops to zero.
Semiconductors
For semiconductors resistance decreases drastically with increasing temperature, as shown on the graph above.
V = R · I
In some educational institutions, it is traditionally written like this U = R · I.
What is important to keep in mind here, is that Ohm's law is an idealized relationship, i.e. it describes the general relation quite well, in regards to metal conductors. However, as a general model for materials, it isn't correct.
Ohm's law can be extended to take the cross-section area, length and the material's conductivity into consideration. For a conductive material, having the cross-section area A, the length ℓ and resistivity ρ, the resistance R is:
| R = ρ · | ℓ |
| A |
Resistivity for a material is defined as the ratio between the electrical field, E, and current density, J:
| ρ = | E |
| J |
The electric field and current density are proportionate at constant temperature, which is the original Ohm's Law, as discovered by G.S. Ohm. The SI unit for ρ is Ω ·m, and the practical aspect of resistivity is that a perfect conductor will have ρ = 0, i.e. no resistance (also called a superconductor), and a perfect insulator, on the other hand, will have ρ = ∞.
Materials following Ohm's Law are called ohmic conductors. Materials not following Ohm's Law are called non-Ohmic conductors.
If we look at resistivity from a practical point of view, these are actual values for some common and representative materials:
| Type | Material | Resistivity at 25 °C (Ω·cm) |
| Conductors | Silver | 1.47·10-8 |
| Copper | 1.72·10-8 | |
| Gold | 2.44·10-8 | |
| Semiconductors | Carbon | 1.47·10-5 |
| Germanium | 6.0·10-1 | |
| Silicon | 2.30·102 | |
| Insulators | Glass | 1010-1014 |
| Mica | 1011-1015 | |
| PVC | 1013-1016 |
Note: Insulator does not mean that the material cannot conduct a current, it means that it is a very poor conductor! The difference becomes relevant when working e.g. with strong current. The line between what is considered a semiconductor and is considered an insulator is not clear, but in practice, line between conductor and semiconductor is around 10−5 Ω·cm, and the transition to insulator is around 107 Ω·cm
Resistivity is dependent on both temperature and material, and you see the following three dependencies:

Metallic conductors
In general for metallic conductors, resistivity increases with temperature. For moderate temperature intervals, the change in resistivity can be calculated using the following approximation:
ρT = ρ0[1 + α(T-T0)]
ρ0 = Resistivity at the reference temperature T0, usually 0 °C or 20 °C
ρT = Resistivity at the temperature T
α = The resistivity's temperature coefficient
This is contrary to e.g. carbon, where resistivity decreases with increasing temperature.ρ0 = Resistivity at the reference temperature T0, usually 0 °C or 20 °C
ρT = Resistivity at the temperature T
α = The resistivity's temperature coefficient
Superconductors
Resistivity decreases with decreasing temperature in the beginning, like for the metals, but at a specific transition temperatures for the material, usually around 0.1 to K, a phase transition occurs in the material and resistivity abruptly drops to zero.
Semiconductors
For semiconductors resistance decreases drastically with increasing temperature, as shown on the graph above.
Conductivity
When working with conductive materials, it often makes more sense using conductivity instead of resistivity. Conductivity, κ (sometimes written as σ) is the reciprocal value of resistivity
For a conductive material the means that
| κ = | 1 |
| ρ |
For a conductive material the means that
| κ = | J | = | ℓ |
| E | R · A |