Ions in solution

For a solution to conduct a current, it has to contain ions. In the classical chemistry this requires chemical compounds that dissociates in water, and that type of conductive solutions is also the subject presented here.

Chemical compounds that by heating, melting and/or dissolving can conduct an electrical current, are called electrolytes. Conductivity is dependent on the concentration, which for acids and bases depends on the degree of dissociation, α. Therefor you divide the electrolytes into strong electrolytes, the ones that dissociates completely, and weak electrolytes, the ones partly dissociating.

For educational purposes, people are used to think of water, and only water, as the solvent, as water normally is a prerequisite for forming ions. In practice, the solvent does not have to be pure water, and for many products, having other liquids mixed in, e.g. ethanol, is quite common. Therefore, aqueous solutions of electrolytes is not the same as the solvent being only water.

A class of molecules called ionic liquids has emerged, which can cause some misunderstandings. Ionic liquids are molecules having a charge without being dissociated and without the presence of water. While being ions they are in effect an electrical conductor like copper and carbon filled plastic.

For aqueous solutions, there is a limit to the resistances you can obtain, as the autoprotolysis provides a concentration of H⁺, actually H₃O⁺, and OH⁻ of 10⁻⁷ M for both. By adding strong electrolytes, the concentration of ions will increase, and resistance decrease. If a current is sent through the solution, the resistance being measured will be dependent on the distance between the electrodes, the surface area of the electrodes (here we presume the electrode have the same surface area) and the type of ions.

The conductance is the reciprocal value of the resistance and is written as S (or L), i.e.

S =	1
	R

The unit for conductance is siemens (S or Ω⁻¹). In older literature one can encounter the name mho (ohm spelled backwards) for Ω⁻¹.

The equation for conductance, taking into consideration the distance between electrodes (d, sometimes called ℓ), the surface area of the electrodes (A), which is the product of the geometrical area times the roughness factor, and conductivity, κ, looks like this:

S = κ ·	A
	d

The electrical conductivity of a solution of electrolytes, κ, is the sum of all ions in the solution. The sum in this case is all properties, i.e. type, concentration, mobility etc.

The ratio d/A is constant for any given measurement, and is called the cell constant, K_cell or θ. The resistance for a solution is something you measure, e.g. using a Wheatstone bridge. Conductivity is inversely proportional with the resistivity of the measuring cell:

κ =	Kcell	= S · Kcell
	R

The cell constant K_cell is determined by measuring the cell's resistance using a solution with a known conductivity. For this you have a number of solutions where the conductivity is known exactly, that can be used. In practice these are premade solutions that you buy for this specific purpose.

The electric mobility is the speed of the charged ions, when a current is running through the solution. Mobility is interesting for several reasons: the electric mobility influences the conductivity, i.e. conductivity for 1 M HCl is different from the conductivity for 1 M KCl, and for batteries, especially rechargeable batteries, reduced mobility has a negative effect on the battery's capacity. For the chemical analysis gel elektrophoresis, the difference in electric mobility is used for separating proteins.

The electrical mobility, μ, for an ion is its drift velocity in the direction of the electrical field, divided by the electric field strength, E:

μ =	dx/dt
	E

The movement of the ions is not a straight line between the two electrodes. Brownian motion sends the ions in random directions, so the drift velocity for the ions is not the speed of the ions themselves, but the average speed with which the ions move in the direction of the electric field.

Mobility is a part of conductivity, which is independent if concentration. Ideally the mobility for a given ion i is:

μi =	| zi | · e
	6 · π · η · Ri

zi	The charge of the ion
Ri	The ion's solvated radius
η	Solvent viscosity
e	The elementary charge constant = 1,602176565(35) · 10-19 C

Conductivity can be written in terms of mobility as:

κ	=	F · ∑ i | zi | · μi · ci
	=	F · ∑ i | zi | ·	(	| zi | · e	)	· ci
				6 · π · η · Ri

Since conductivity is dependent on concentration, you have to have a way of comparing the ions. For this you have the molar conductivity, Λ, which is the conductivity, κ, divided by the total ionic concentration, C:

Λ =	κ
	C

Under ideal conditions, you should get the same Λ value for a chemical compound no matter what concentration you are measuring at. But, as not all electrolytes are strong, and the ions influence each other in solution, this is not the case. Therefore, you have the Λ⁰, which is the molar conductivity at infinite dilution. The infinite dilution and the practical aspect of this, will be described further down.

At the ideal infinite dilution a chemical compound is fully dissociated, i.e. α=1, and the relation between Λ, Λ⁰ and α is this:


Λ⁰ for an electrolyte is equal to the sum of the electrolyte's components. This is Kohlrausch' law. In practice, this means that for the electrolyte A_aB_b, it looks like this:


One way of writing this, which is commonly used, is:


The use of Λ and λ for conductivity in educational material is somewhat erratic, which may lead to some confusion. For this material, the common international notation is used.

Many λ⁰ can be found in reference books, e.g.

Λ0(Ag2CO3)	= 2 · λ0(Ag+) + λ0(CO32−)
	= 2·61.9 S·cm²/mol + 138.6 S·cm²/mol
	= 262.4 S·cm²/mol

The concept infinite dilution is a misnomer, as an infinite dilution would end up with a measurement on pure solvent, for all electrolytes.

In practice, the value determined for Λ⁰ is an extrapolation from a number of measurements, to the y-axis (0 mol/l), i.e. you do a number of conductivity measurements, calculate Λ, and insert the measurements in a coordination system. For KCl and acetic acid (HAc), you get something like this (model, not actual measurements):



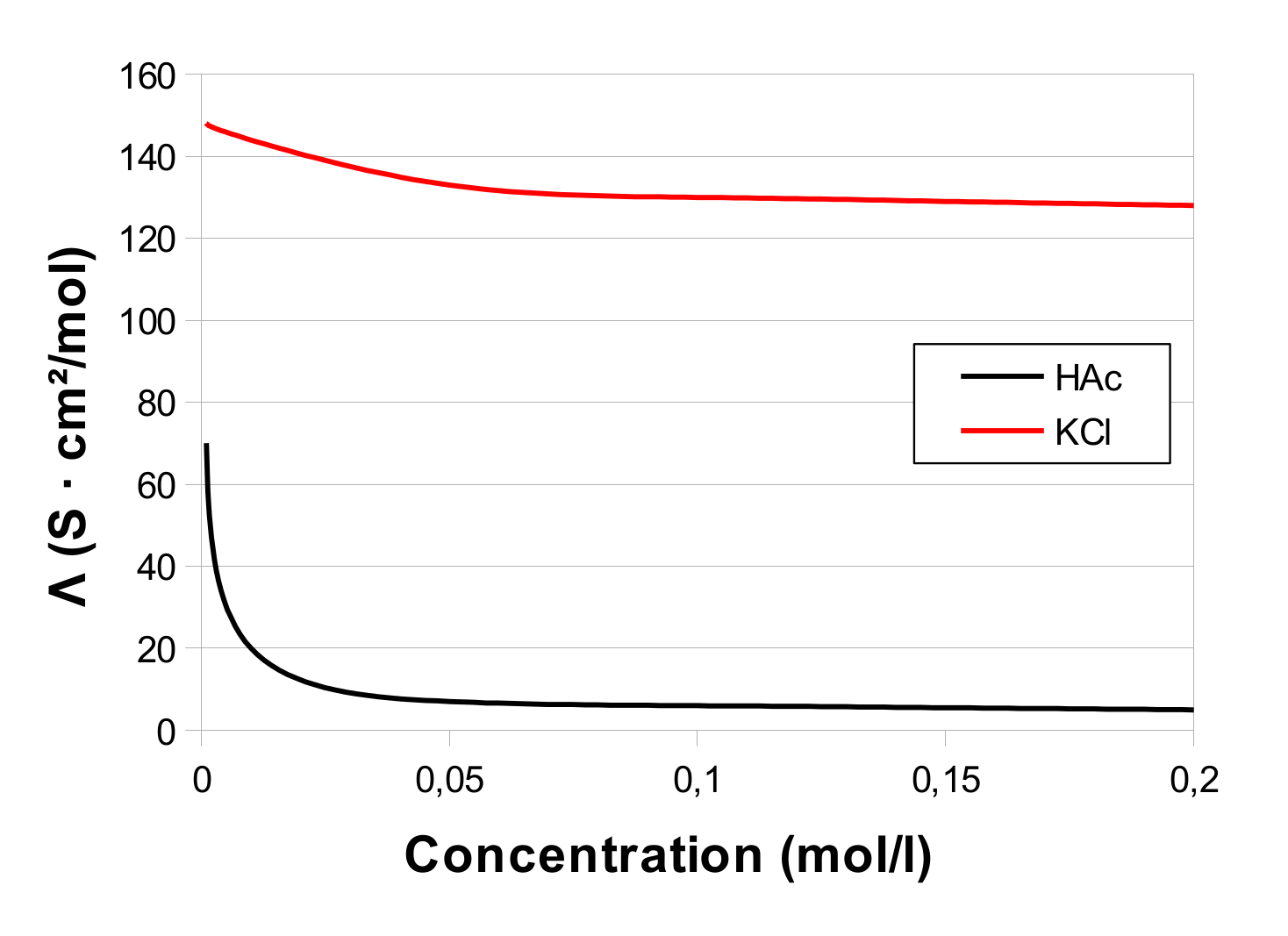
For KCl you will, by extrapolating to the y-axis, be able to get the correct value 149.9 S · cm²/mol, while for HAc you have no way of hitting the correct value of 390.7 S · cm²/mol.

This example also demonstrates quite well why you don't determine Λ⁰ for weak electrolytes by direct measurements.

If we are working with weak electrolytes, i.e. chemical compounds that doesn't dissociate completely, e.g. weak acids, measuring directly on the dilutions is not the way to do it. You can do the measurements, but, as demonstrated above, if you want a result that is accurate/useful, you need to use a small workaround.

For educational use, the preferred example is the determination of Λ⁰ for acetic acid, as it is also quite good for lab exercises:

For acetic acid:

Λ⁰(HAc) = λ⁰(H⁺) + λ⁰(Ac⁻)

If you add Λ⁰(NaCl) on both sides, you can do a bit of mathematical rearrangement:

Λ⁰(HAc) + Λ⁰(NaCl) = λ⁰(H⁺) + λ⁰(Ac⁻) + Λ⁰(NaCl)
Λ⁰(HAc) + Λ⁰(NaCl) = λ⁰(H⁺) + λ⁰(Ac⁻) + λ⁰(Na⁺) + λ⁰(Cl⁻)
Λ⁰(HAc) + Λ⁰(NaCl) = Λ⁰(HCl) + λ⁰(Ac⁻) + λ⁰(Na⁺)
Λ⁰(HAc) + Λ⁰(NaCl) = Λ⁰(HCl) + Λ⁰(NaAc)
Λ⁰(HAc) = Λ⁰(HCl) + Λ⁰(NaAc) - Λ⁰(NaCl)

So, by measuring the molar conductivity for HCl, NaAc and NaCl, which are all strong electrolytes, you can determine the molar conductivity for the weak electrolyte acetic acid.